以前、「回帰分析とは何か?」「単回帰分析でわかること」を解説しました。
しかし、Excel”データ分析”ツールには、”単”も”重”もなく、選択できるのは”回帰分析”のみです。
「結果に影響を与えそうだ」と推定される”説明変数”が1つのものが単回帰分析、複数つかうのが重回帰分析です。
以前の記事では、「実収入」(説明変数)と「実支出」(目的変数)の関係を、単回帰分析してみました。これに、「家計貯蓄」という2つめの説明変数が追加されると、重回帰分析になります。
以上!!
といってしまっては、あまりにもあっけなさすぎます。
それに、「収入の高い方が、支出も多い傾向がある」というのは、わざわざ分析ツールにかけなくても、想像しやすい傾向ですよね。
そこで、この記事では、別の事例をとおして、複数の説明変数をつかい重回帰分析をしてみましょう。
住みやすく、大学進学率の高い地域には、肥満者が少ないのか?
突然ですが、見出しにあげた肥満者割合の仮説は、正しいでしょうか? 正しくないでしょうか?
正しくはありません。
国内47都道府県を比較するなら、説明変数(住みやすさ、大学進学率)、目的変数(肥満者の比率)が、すべてWeb上に公開されていますので、これらのデータをExcelで重回帰分析してみると、よくわかります。
<今回使用した各データの出典>
(1)住みたい都道府県ランキング2020【47都道府県・完全版】
(2)学校基本調査(令和2年度「高等学校_卒業後の状況調査」より)
(3)平成28年国民健康・栄養調査報告
(BMI25以上を肥満者として、肥満者比率が高い順の都道府県別ランキング)
(3)調査について、調査時に熊本地震の影響があったため、熊本県をのぞく結果が公開されました。そこで、以下の回帰分析では、「熊本県をのぞく46都道府県」の比較をしています。 まず、3つの都道府県別公開データを、同一のExcelワークシートにまとめて[データ分析]→[回帰分析]を選択します。
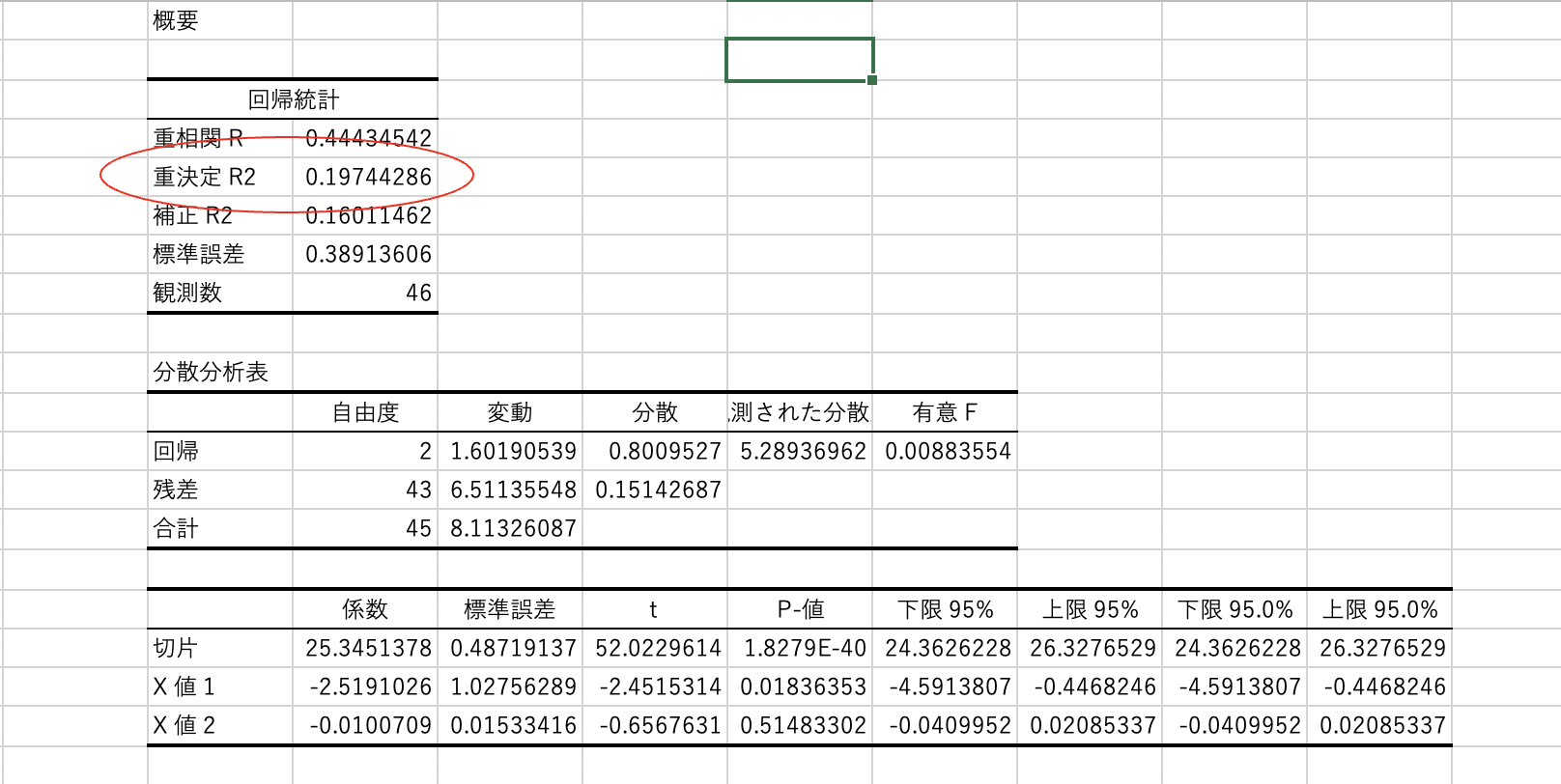
やはり、決定係数(重決定R2)は0.19で、住みやすさや大学進学率と、”肥満者”との間には、あまり関係はなさそうですね(一般に、重決定R2指数が0.4以上で、”関係性が強い”とみなされます)。
しかし、これは説明変数に「住みやすさ」と「大学進学率」をつかったために、わからなくなってしまった結果なのです。
視覚的に確認するため、(1)住みやすさ-高BMI地域と、(2)大学進学率-高BMI地域の2軸を比較する散布図を作成してみましょう。
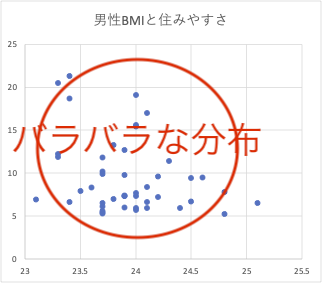
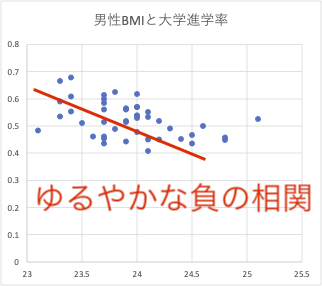
”「住みやすさ」は地域の肥満度と全く関係がない”のですが、大学進学率と地域肥満度には、”ゆるやかな負の相関”(進学率が高い地域ほど、肥満者の比率が低い)がみられるのです。
なぜ、進学率があがると、肥満者の比率がさがるのか? ここから先は、また別の仮説検証をして、因果関係を明らかにする必要があります。この記事では、そこまで深ぼりしませんが、この点について、大学や各種研究機関などで調査した結果も、Web上に複数公開されています(参考「都道府県別の肥満者割合と社会経済格差について」)ので、参照してみてください。
マッキンゼー流”完全無欠の問題解決”も、Excel重回帰分析から
なぜ、「住みやすさ」「進学率」と「肥満度」という、一見、関係なさそうな変数で重回帰分析をしたかというと、これが【マッキンゼー流】らしいからです。
完全無欠の問題解決―――不確実性を乗り越える7ステップアプローチ(https://amzn.to/3fbGBwN)
本書のエッセンスが、「マッキンゼーの元パートナーが回帰分析で肥満を分析してみた」にも紹介されています。一部を引用すると、
回帰分析の結果、教育、収入、街の歩きやすさ、快適性スコアのすべてが肥満と負の相関にあることを示した。また、歩きやすさを除くすべての変数が、個別に肥満と相関していることを発見した。
おそらく驚くべきことに、快適性スコアと歩きやすさの間にはほとんど相関がなかった。他の変数、特に収入と教育の間には高い相関があり(68%)、因果関係における相対的な影響度合を判定することが難しくなる可能性を示していた。(DIAMOND onlineより)
米国人著者が、アメリカ地域特性として紹介した事例も、日本の都道府県別で分析しなおせる、”再現性が高いアプローチ”だということをご紹介しました。このマッキンゼー流分析を応用すれば、
「自宅の屋根にソーラーパネルを設置すべきか」「老後のためにどれだけ貯金すればいいか」といった個人の問題から、「販売価格を上げるべきか」「ITの巨人に訴訟を挑んでいいか」といったビジネス上の問題まで (DIAMOND onlineより)
机上でシミュレーションしてみることができますよ。
まとめ
重回帰分析のおもしろみは、関係なさそうな指標のくみあわせで
意外な関係性や法則を見つけること
Excel[データ分析]をつかえば、回帰分析のために複雑な計算式をおぼえる必要はありません。ただ、比較する資料を集めてきて、ウィザードにそって「説明変数」と「目的変数」を指定すればよいだけです。
しかも、分析結果が的はずれなものであっても、元のデータが加工されてしまうわけではないので、何度でも別の切り口から分析をやりなおせるのです。
さまざまなデータと比較すれば、「え! こんな指標が説明変数(事件・事故や課題の原因)になるなんて…」という意外な発見があるかもしれません。それが、複数の説明変数をつかう重回帰分析のおもしろみでもあります。
“マッキンゼー流、完全無欠の問題解決”も、まずはコツコツExcel重回帰分析から!
自分の仕事でよくつかうデータのくみあわせにおきかえて、ぜひ”新しい発見”を楽しんでみてください。